

Since the Covid pandemic, I really got into D&D. I had never played before, but had friends who had long lasting parties and were DMs, so it was the perfect opportunity since we were all locked up in our houses.
Turns out that it didn’t last more than a few months: we started one campaign at level 1 and disbanded shortly after reaching level 6. Then I found out about Critical Role and became a huge fan (although I’ve given up on Campaign 3…) and started playing with my partner and his friends.
As you can imagine, it wasn’t too long before I started DMing myself and I eventually started watching some of Matt Colville’s Twitch lives and YouTube videos (really recommend those for DMs!). So when Matt’s company MCDM started designing their own RPG, I was pretty excited (if you want to know more about it, you can listen to the podcast The Dice Society, which covers news on the development of the game).
For me, the game changer for this new RPG is the dice. Everyone who plays D&D, be it 5th edition, AD&D or anything in between, is used to rolling d20s, 20-sided dice1. On the other hand, MCDM’s RPG uses 2 regular, 6-sided dice for attacking, making ability checks and other situations in which your character might need to roll. As of now (March 2024), the game is still in development, so it still might change, but they made it very clear that they want to keep the 2d6 system in the final version of the game.
Why I love the idea of the 2d6 system
I know: d6s are kind of boring compared to d20s, right? Every Farkle and Yahtzee player uses them, after all. But to me, that could be a great advantage: it’s easy to understand and hit the ground running as soon as you know the basic rules, no need to go through weird dice2.
And although I’ve become some sort of dice hoarder for the past years, I love the idea of rolling two dice, and more than that, two d6s, because of variance.
Let’s assume we’re rolling a d20. The possible outcomes range from 1 to 20, and tecnically they all have the same probability, 1/20 = 5%. When rolling 2d6, there is a smaller range of possibilities (2 to 12) and they are not uniformally probable (you would expect to roll 12 much less frequently than 7, for example).
That means your modifier has a much more significant impact on the final result than sheer luck3. If you are consistently rolling some value near the mean (7), how good you are at a certain ability will more accurately translate to how successful you are in a skill check or attack. Sure, you can still fumble or do exceptionally well, but those events are less common.
Simulating dice rolls
I remember when I was younger and my Math teacher gave us an experiment: roll two dice 100 times and take note of the results. At the end of the class, we drew a bar plot with the results and found out that everyone drew basically the same plot.
Let’s do the same, but with the RPG context and in a larger scale. We’ll check how the outcome of a character with a dexterity bonus of +3 would roll for a skill check using different dice systems. (MCDM’s stats are not exactly the same, but let’s just assume they are for this thought exercise.)
Rolling 1d20 1000 times
Assuming that every side on a 20-sided die is physically the same, it’s fair to conclude that the numbers 1 through 20 have the same probability of being the outcome. Let’s imagine that we’re rolling the die 100 times and counting how many times each side appears.
Now let’s do the same, rolling the die 1000 times.

The results seem random enough and there doesn’t seem to be a clear pattern. Even if we add the modifier (+3), it’s not that great a difference. The modifier matters much less then the roll of a die.
As a game design, it makes sense that extremely good (or bad) results are rare, but it’s weird that average outcomes are equally probable.
Rolling 2d6 1000 times
If we were rolling only one d6, we would have a similar situation: all 6 sides have the same probability. However, by adding two dice, we invoke the Central Limit Theorem!
What is that, you ask? It’s one of the most important theorems in probability theory that says that, given a sample from a random variable under certain circumstances, the sample mean tends to follow a normal distribution, even if the original variable has a different distribution other than normal. More technically, the limit of a random variable X when n -> Inf is normally distributed. More on that in the next section.
For now, let’s replicate the experiment we did with the d20, this time with 2d6.
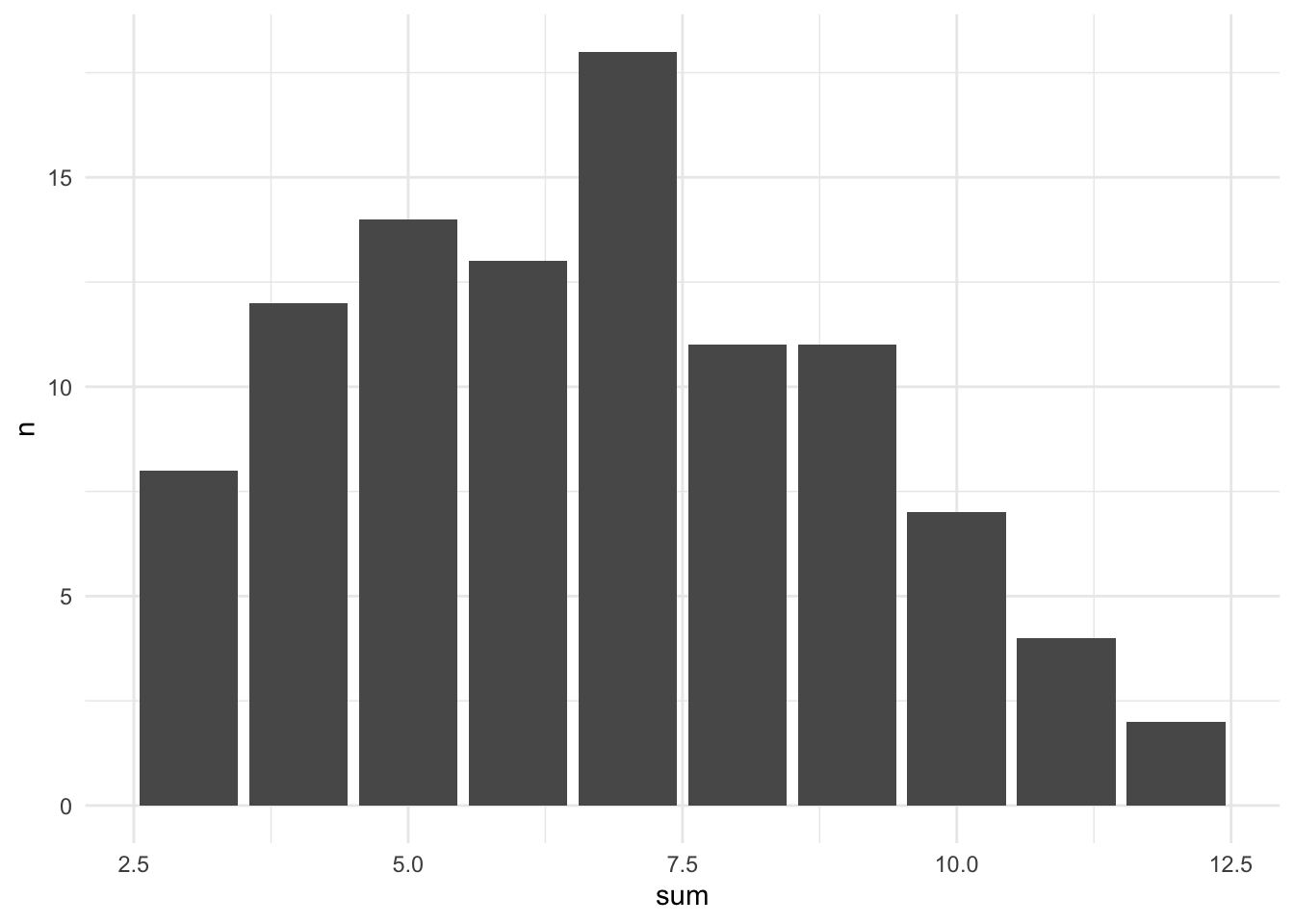
This plot shows what we’ve talked before: it’s much more common to roll a 7 than, say, a 12. The same goes for the other end of the curve, too.
Now let’s take a look at what happens if we increase the number of rolls to a thousand:
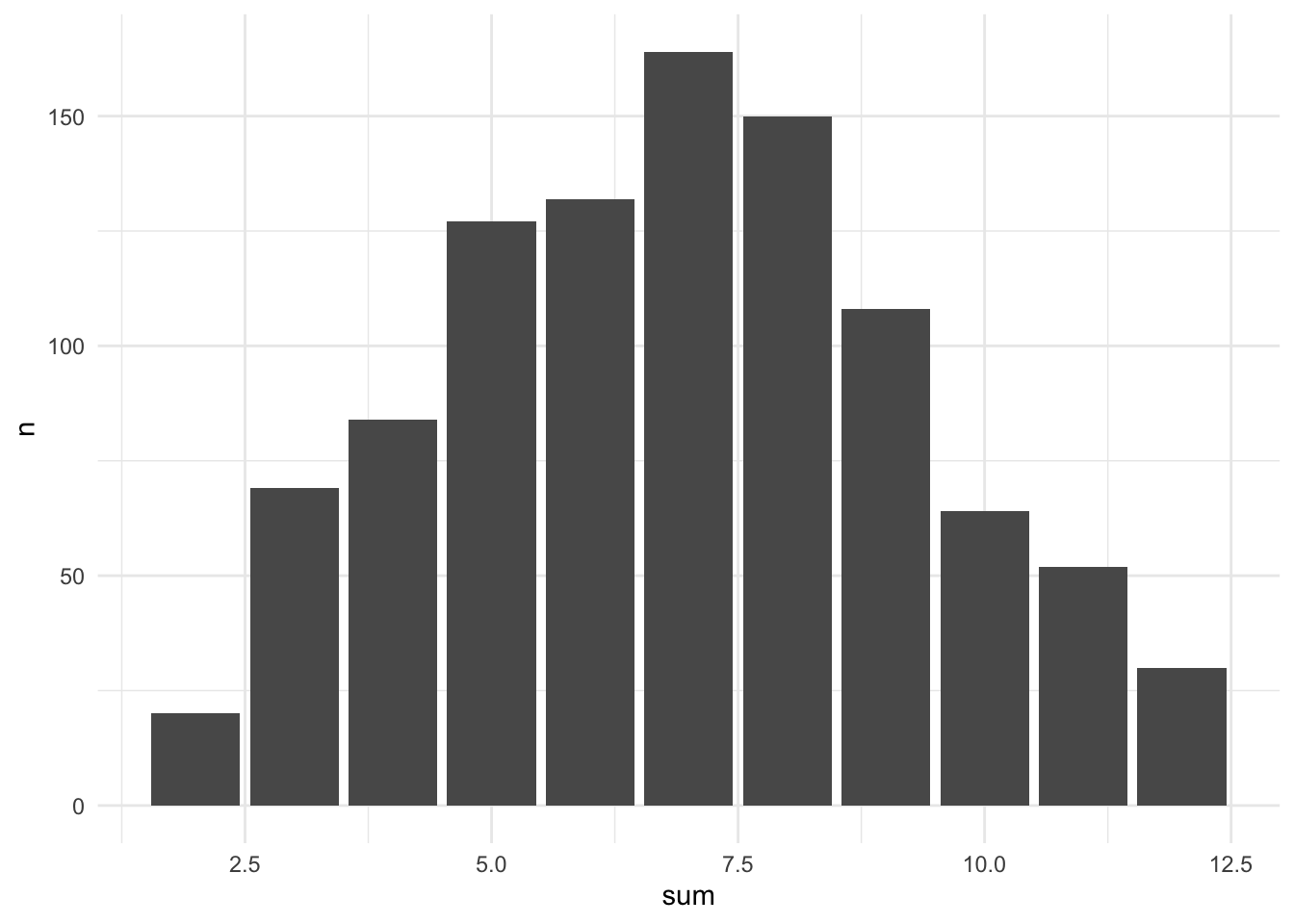
And a million:

The math behind it: the Central Limit Theorem
If you are not convinced by this little experiment, the proof for the theorem can be easily found online.
I’m not going to bore you with the details because 1, this is not the place for it and 2, I’m not ashamed to admit that I don’t even remember the proof and would just copy it from someplace else anyway.
Balancing predictability and uncertainty
So why does a more consistent result = a better game? (To me, at least.)
Of course it’s fun to have some unpredictability when we’re playing, otherwise we would simply discard the dice. But it’s always frustrating when you know that your character is very good in a skill but you KEEP. ROLLING. ONES.
As a DM, it’s also hard to explain why that keeps happening in a way that makes sense narratively. “Oh, you see that the door is completely rotten but you simply can’t break it despite your Strength (20)” More especifically about D&D, it also creates some significant differences for classes such as Bard and Rogue.
I think only time will tell if MCDM’s 2d6 system works for me in the long run. But for now, I’m excited about changing things up a little and depending a little less on my misbehaving dice.
Footnotes
Despite being used in older editions, d20s started being the default dice starting at D&D 3rd edition.↩︎
I hate to admit it, but I still confuse my d20s and d12s on occasion.↩︎
Tom Dunn has written a great series analyzing variability which I highly recommend in The Finished Book.↩︎